Methodology (Part I)
The first part of this project aims at writing a Python program that helps investors to implement the variance-minimization strategy on a two-stocks portfolio. Data collection is one of the most challenging parts of writing this Python program.
Step I: removing dates
I first obtain weekly closing prices of twenty stocks from 4/24/2009 to 4/27/2012 using Google finance. The following is a snapshot of the original excel file:
The first part of this project aims at writing a Python program that helps investors to implement the variance-minimization strategy on a two-stocks portfolio. Data collection is one of the most challenging parts of writing this Python program.
Step I: removing dates
I first obtain weekly closing prices of twenty stocks from 4/24/2009 to 4/27/2012 using Google finance. The following is a snapshot of the original excel file:
To remove the dates on every alternate column, I wrote a function in Python named removeDates(). removeDates() reads the CSV file of the above data into a string and splits this string into a lists of lists. Then, removeDates() uses a for loop to remove all the dates except those in the first column and output a CSV file called WeeklyStockPrices_NoDates.csv. After removing the dates, the data appear in Excel as follow:
Step II: calculating weekly return and variance of weekly return
In this step I used Excel to read the CSV file generated in the Step I. Then I used the following formula to compute the weekly rate of return:
(Closing of current week – closing price of previous week) / closing price of previous week
I used the variance function in Excel to calculate the variance of stock returns over the three year period from 2009 to 2012; for example, =VAR(B3:B159) gives me the stock variance for AAPL (Apple Inc.) over the three year period. Finally, I export the weekly stock returns and stock variances as a CSV file named WeeklyReturn.csv.
Step III: calculating correlation between stock return
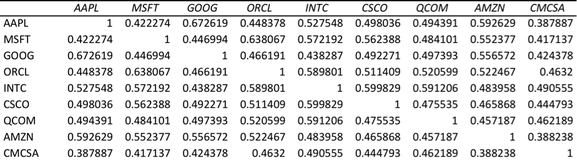
From the stock returns data generated in Step II, I also calculated the correlation between stock returns of all twenty stock using Excel’s data analysis tool pack. A snapshot of the correlation table appears as follow:
In this step I used Excel to read the CSV file generated in the Step I. Then I used the following formula to compute the weekly rate of return:
(Closing of current week – closing price of previous week) / closing price of previous week
I used the variance function in Excel to calculate the variance of stock returns over the three year period from 2009 to 2012; for example, =VAR(B3:B159) gives me the stock variance for AAPL (Apple Inc.) over the three year period. Finally, I export the weekly stock returns and stock variances as a CSV file named WeeklyReturn.csv.
Step III: calculating correlation between stock return
From the stock returns data generated in Step II, I also calculated the correlation between stock returns of all twenty stock using Excel’s data analysis tool pack. A snapshot of the correlation table appears as follow:
Step IV: Writing the Python program to find variance-minimizing strategy
I wrote a Python function minPortfolioVariance(stockA, stockB) to return the asset allocation that minimizes the portfolio variances for a two-stocks portfolio composed of stock A and stock B. minPortfolioVariance(stockA, stockB) calls another function named calculatePortVar(stockA, stockB) to calculate the portfolio variance under each scenario. The portfolio variance is calculated using the following formula:
Portfolio Variance = WeightA2(VarA)+ WeightB2(VarB) + 2*WeightA(WeightB)(CorrA,B)√(VarA)(VarB)
where
WeightA stands for the weight of the portfolio on stock A (eg. portfolio worth $100 in total, and $10 is invested in stock A, then WeightA = 0.1);
VarA stands for the variance of weekly returns of stock A (obtained from Step II);
CorrA,B stands for the correlation coefficient between weekly returns of stock A and stock B (obtained from Step III).
minPortfolioVariance(stockA, stockB) uses a for loop to go through all the scenarios when from weightA = 0.05, to weightA = 0.10, to weightA = 0.15,……, to weightA = 0.95. minPortfolioVariance (stockA, stockB) eventually returns the value of weightA and weightB that give the smallest portfolio variance.
I wrote a Python function minPortfolioVariance(stockA, stockB) to return the asset allocation that minimizes the portfolio variances for a two-stocks portfolio composed of stock A and stock B. minPortfolioVariance(stockA, stockB) calls another function named calculatePortVar(stockA, stockB) to calculate the portfolio variance under each scenario. The portfolio variance is calculated using the following formula:
Portfolio Variance = WeightA2(VarA)+ WeightB2(VarB) + 2*WeightA(WeightB)(CorrA,B)√(VarA)(VarB)
where
WeightA stands for the weight of the portfolio on stock A (eg. portfolio worth $100 in total, and $10 is invested in stock A, then WeightA = 0.1);
VarA stands for the variance of weekly returns of stock A (obtained from Step II);
CorrA,B stands for the correlation coefficient between weekly returns of stock A and stock B (obtained from Step III).
minPortfolioVariance(stockA, stockB) uses a for loop to go through all the scenarios when from weightA = 0.05, to weightA = 0.10, to weightA = 0.15,……, to weightA = 0.95. minPortfolioVariance (stockA, stockB) eventually returns the value of weightA and weightB that give the smallest portfolio variance.